اعداد اول مرسن اعداد اولی به فرم  هستند که به افتخار نام کشیش فرانسوی مارین مرسن (به انگلیسی: Marin Mersenne)، به این نام خوانده میشوند. چرا که مرسن در زمینهٔ اول بودن این نوع اعداد اظهار نظری نادرست اما محرک کرده بود. اولین اعداد مرسن اعداد زیر هستند: ۳, ۷, ۳۱, ۱۲۷, ۸۱۹۱, ۱۳۱۰۷۱, ۲۱۴۷۴۸۳۶۴۷ و ... که متناظر هستند با ... ,۸۹ ,۶۱ ,۳۱ ,۱۹ ,۱۷ ,۱۳ ,۷ ,۵ ,۳ ,۲ =n
هستند که به افتخار نام کشیش فرانسوی مارین مرسن (به انگلیسی: Marin Mersenne)، به این نام خوانده میشوند. چرا که مرسن در زمینهٔ اول بودن این نوع اعداد اظهار نظری نادرست اما محرک کرده بود. اولین اعداد مرسن اعداد زیر هستند: ۳, ۷, ۳۱, ۱۲۷, ۸۱۹۱, ۱۳۱۰۷۱, ۲۱۴۷۴۸۳۶۴۷ و ... که متناظر هستند با ... ,۸۹ ,۶۱ ,۳۱ ,۱۹ ,۱۷ ,۱۳ ,۷ ,۵ ,۳ ,۲ =n
اثبات چند قضیه کاربردی در این رابطه
قضیه اول: اگر  اول باشد،
اول باشد،  نیز باید خود اول باشد.
نیز باید خود اول باشد.
اثبات: فرض کنیم که حکم نادرست است (برهان خلف). یعنی به ازای  مرکبی،
مرکبی، 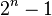 اول است؛ در این صورت میتوان
اول است؛ در این صورت میتوان  را به صورت ضرب دو عدد غیر یک
را به صورت ضرب دو عدد غیر یک  نوشت. پس:
نوشت. پس:
 پس اگر
پس اگر  زوج باشد، طبق اتحاد مزدوج و اگر فرد باشد طبق اتحاد چاق و لاغر (لاگرانژ) به عوامل اول تجزیه میشود و اول نیست؛ پس به تناقض میرسیم و فرض خلف باطل است. پس
زوج باشد، طبق اتحاد مزدوج و اگر فرد باشد طبق اتحاد چاق و لاغر (لاگرانژ) به عوامل اول تجزیه میشود و اول نیست؛ پس به تناقض میرسیم و فرض خلف باطل است. پس  باید اول باشد.
باید اول باشد.
اعداد مرسن واعداد کامل(تام)
بدیهی است که اعداد مرسن در مبنای دو به صورت  میباشد که برابر
میباشد که برابر  است (
است ( تا یک).
تا یک).
تعریف: عدد کامل (تام) عددی است که با مجموع مقسوم علیههای خود، به جز خودش، برابر باشد. از معروفترین آنها ۶=۳+۲+۱ و ۲۸=۱۴+۷+۴+۲+۱ هستند.
قضیه دوم: هر عدد کامل به صورت  است که
است که  اول است.
اول است.
اینها اعداد به شکل  مرسن هستند و متعاقباً توانهای آنها (
مرسن هستند و متعاقباً توانهای آنها ( )اول است. پس با یافتن هر عدد کامل، میتوان یک عدد مرسن جدید پیدا کرد.
)اول است. پس با یافتن هر عدد کامل، میتوان یک عدد مرسن جدید پیدا کرد.
آزمایش لوکاس- لمر
تقسیم آزمایشی اکثراً برای تصدیق مرکب بودن یک عدد مرسن اول پنهان استفاده میشود. این آزمایش فوراً نشان میدهد که  به ازای
به ازای  مرکب است (به ترتیب با عوامل اول ۲۳، ۴۷، ۱۶۷، ۲۶۳، ۳۵۹، ۳۸۳، ۴۷۹ و ۵۰۳).
مرکب است (به ترتیب با عوامل اول ۲۳، ۴۷، ۱۶۷، ۲۶۳، ۳۵۹، ۳۸۳، ۴۷۹ و ۵۰۳).
یک آزمایش بسیار قدرتمند اولیه برای شناسایی  آزمایش لوکاس- لمر است.
آزمایش لوکاس- لمر است.
ابتدا سه قضیه زیر را مطرح میکنیم:
- اگر
 به پیمانه ۴ و
به پیمانه ۴ و  عدد اول باشد، در این صورت
عدد اول باشد، در این صورت  ، اگر
، اگر 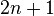 اول باشد.
اول باشد.
- همچنین این درست است که عوامل اول
 باید شکل
باید شکل 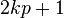 داشته باشند که
داشته باشند که  یک عدد مثبت طبیعی است و در عین حال شکل
یک عدد مثبت طبیعی است و در عین حال شکل  یا
یا  را داشته باشد (آسپنسکی و هیسلت ۱۹۳۹).
را داشته باشد (آسپنسکی و هیسلت ۱۹۳۹).
- یک عامل اول
 از یک عدد مرسن
از یک عدد مرسن 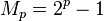 (چه اول و چه مرکب) در صورتی عدد ویفریچ اول است که
(چه اول و چه مرکب) در صورتی عدد ویفریچ اول است که 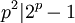 . بنابراین یک عدد مرسن نمیتواند عدد ویفریچ اول باشد.
. بنابراین یک عدد مرسن نمیتواند عدد ویفریچ اول باشد.
آیا عدد کامل فرد وجود دارد؟
میدانیم تمام اعداد کامل به صورت حاصل ضرب یک عدد اول مرسن توانی از دو میباشند؛ اما در مورد اعداد فرد کامل چه نظریهای وجود دارد؟ اگر این چنین عددی وجود داشته باشد در این صورت، به صورت حاصل ضرب یک مربع کامل در یک عدد اول به توان فرد میباشد، این عدد حداقل هشت عامل اول دارد و حداقل بر ۳۷ عدد اول بخش پذیر است (لزومی ندارد که متمایز باشند)؛ این عدد حداقل در مبنای اعشاری ۳۰۰ رقم دارد؛ و یک مقسوم علیه اول بزرگ تر از ۱۰۲۰ دارد.
آیا تعداد اعداد مرسن بی نهایت است؟
این سوال معادل با پاسخ دادن به این سوال است که آیا تعداد نامحدودی عدد کامل زوج است. جواب این است که احتمالاً بله است (زیرا سری هارمونیک واگراست).
آیا تعداد اعداد مرسن مرکب بی نهایت است؟
نظریه اولر: اگر  باشد و
باشد و  اول باشد، در این صورت
اول باشد، در این صورت 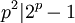 نیز اول است، اگر و تنها اگر باقیمانده تقسیم
نیز اول است، اگر و تنها اگر باقیمانده تقسیم  بر
بر 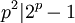 برابر
برابر  باشد.
باشد.
همچنین اگر  باشد و
باشد و 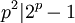 اول باشد، در این صورت عدد مرسن
اول باشد، در این صورت عدد مرسن 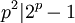 مرکب است (این حدس احتمالاً منطقی است از آن جایی که تعداد اعداد اولی که به ازای
مرکب است (این حدس احتمالاً منطقی است از آن جایی که تعداد اعداد اولی که به ازای  به صورت
به صورت  باشد، بی نهایت است.
باشد، بی نهایت است.
 هر عدد طبیعی فرد باشد؛ در این صورت اگر دو شرط اول -که در زیر آمده است- برقرار باشد، گزاره سوم برقرار خواهد بود:
هر عدد طبیعی فرد باشد؛ در این صورت اگر دو شرط اول -که در زیر آمده است- برقرار باشد، گزاره سوم برقرار خواهد بود: ,
,
 عدد اول باشد (بدیهی است که عدد مرسن اول است.).
عدد اول باشد (بدیهی است که عدد مرسن اول است.). عددی اول است.
عددی اول است. بر یک عدد مرسن تقسیم شود، در این صورت
بر یک عدد مرسن تقسیم شود، در این صورت  یک عدد اول ویفریچ است و این اعداد کمیاب هستند! فقط دو عدد شناخته شدهاند که زیر 4,000,000,000,000 هستند و هیچ کدام از این مربعها بر یک عدد مرسن بخش پذیر نیستند.
یک عدد اول ویفریچ است و این اعداد کمیاب هستند! فقط دو عدد شناخته شدهاند که زیر 4,000,000,000,000 هستند و هیچ کدام از این مربعها بر یک عدد مرسن بخش پذیر نیستند. و
و 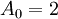 آیا همه این دنباله اول هستند؟ دیکسون کاتالان، در پاسخ این سؤال در سال 1876، به لوکاس اظهار داشت که 1-127^2 (
آیا همه این دنباله اول هستند؟ دیکسون کاتالان، در پاسخ این سؤال در سال 1876، به لوکاس اظهار داشت که 1-127^2 (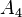 )، به این ترتیب اول است. همان طور که مشخص است این اعداد در این دنباله بسیار سریع بزرگ میشوند:
)، به این ترتیب اول است. همان طور که مشخص است این اعداد در این دنباله بسیار سریع بزرگ میشوند:
 هستند که به افتخار نام کشیش فرانسوی مارین مرسن (به انگلیسی: Marin Mersenne)، به این نام خوانده میشوند. چرا که مرسن در زمینهٔ اول بودن این نوع اعداد اظهار نظری نادرست اما محرک کرده بود. اولین اعداد مرسن اعداد زیر هستند: ۳, ۷, ۳۱, ۱۲۷, ۸۱۹۱, ۱۳۱۰۷۱, ۲۱۴۷۴۸۳۶۴۷ و ... که متناظر هستند با ... ,۸۹ ,۶۱ ,۳۱ ,۱۹ ,۱۷ ,۱۳ ,۷ ,۵ ,۳ ,۲ =n
هستند که به افتخار نام کشیش فرانسوی مارین مرسن (به انگلیسی: Marin Mersenne)، به این نام خوانده میشوند. چرا که مرسن در زمینهٔ اول بودن این نوع اعداد اظهار نظری نادرست اما محرک کرده بود. اولین اعداد مرسن اعداد زیر هستند: ۳, ۷, ۳۱, ۱۲۷, ۸۱۹۱, ۱۳۱۰۷۱, ۲۱۴۷۴۸۳۶۴۷ و ... که متناظر هستند با ... ,۸۹ ,۶۱ ,۳۱ ,۱۹ ,۱۷ ,۱۳ ,۷ ,۵ ,۳ ,۲ =n اول باشد،
اول باشد،  نیز باید خود اول باشد.
نیز باید خود اول باشد.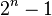 اول است؛ در این صورت میتوان
اول است؛ در این صورت میتوان  نوشت. پس:
نوشت. پس: پس اگر
پس اگر  زوج باشد، طبق اتحاد مزدوج و اگر فرد باشد طبق اتحاد چاق و لاغر (لاگرانژ) به عوامل اول تجزیه میشود و اول نیست؛ پس به تناقض میرسیم و فرض خلف باطل است. پس
زوج باشد، طبق اتحاد مزدوج و اگر فرد باشد طبق اتحاد چاق و لاغر (لاگرانژ) به عوامل اول تجزیه میشود و اول نیست؛ پس به تناقض میرسیم و فرض خلف باطل است. پس  میباشد که برابر
میباشد که برابر  است (
است ( است که
است که  اول است.
اول است. به ازای
به ازای  مرکب است (به ترتیب با عوامل اول ۲۳، ۴۷، ۱۶۷، ۲۶۳، ۳۵۹، ۳۸۳، ۴۷۹ و ۵۰۳).
مرکب است (به ترتیب با عوامل اول ۲۳، ۴۷، ۱۶۷، ۲۶۳، ۳۵۹، ۳۸۳، ۴۷۹ و ۵۰۳). به پیمانه ۴ و
به پیمانه ۴ و  ، اگر
، اگر 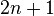 اول باشد.
اول باشد.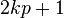 داشته باشند که
داشته باشند که  یک عدد مثبت طبیعی است و در عین حال شکل
یک عدد مثبت طبیعی است و در عین حال شکل  یا
یا  را داشته باشد (آسپنسکی و هیسلت ۱۹۳۹).
را داشته باشد (آسپنسکی و هیسلت ۱۹۳۹).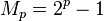 (چه اول و چه مرکب) در صورتی عدد ویفریچ اول است که
(چه اول و چه مرکب) در صورتی عدد ویفریچ اول است که 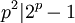 . بنابراین یک عدد مرسن نمیتواند عدد ویفریچ اول باشد.
. بنابراین یک عدد مرسن نمیتواند عدد ویفریچ اول باشد. باشد و
باشد و  اول باشد، در این صورت
اول باشد، در این صورت  بر
بر  باشد.
باشد. باشد، بی نهایت است.
باشد، بی نهایت است.
 داریم
داریم 

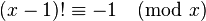
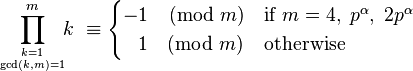
 عددی صحیح و مثبت است.
عددی صحیح و مثبت است.














 که 10و8و6 هستند. این موضوع با تمام مضارب دیگر نیز برقرار خواهد بود.
که 10و8و6 هستند. این موضوع با تمام مضارب دیگر نیز برقرار خواهد بود.